Voilà, l’été est bientôt fini, les matins gris sont déjà là et l’année scolaire va commencer (bon OK… j’anticipe à peine!). Et comme une mauvaise nouvelle n’arrive jamais seule, ceux d’entre vous qui auront gardé la spécialité mathématiques en terminale risquent fort de commencer avec le raisonnement par récurrence. Voici de quoi vous aider pour ce début d’année.

Le but de l’article du jour est de vous familiariser avec ce genre de raisonnement en vous donnant un guide à suivre scrupuleusement (au moins dans un premier temps).

D’abord, un raisonnement par récurrence, c’est quoi? Cela fait quelques années maintenant que le prof de maths vous martèle l’idée que pour faire une démonstration il ne faut pas prendre de valeurs particulière mais bien démontrer pour toutes les valeurs possibles (d’où l’intérêt de l’utilisation des lettres). Sauf que parfois, c’est pas évident de démontrer pour tout n. Le raisonnement par récurrence est là pour vous y aider (sisi! pour vous aider!). L’idée de base est finalement assez simple. Prenons un escalier, le but est de savoir si vous pourrez monter toutes les marches (oui, j’ai bien écrit TOUTES les marches). On va utiliser l’idée suivante: Si je peux monter sur la première marche ET que lorsque je suis sur une marche je peux monter sur la suivante… ALORS je peux monter sur n’importe quelle marche. 

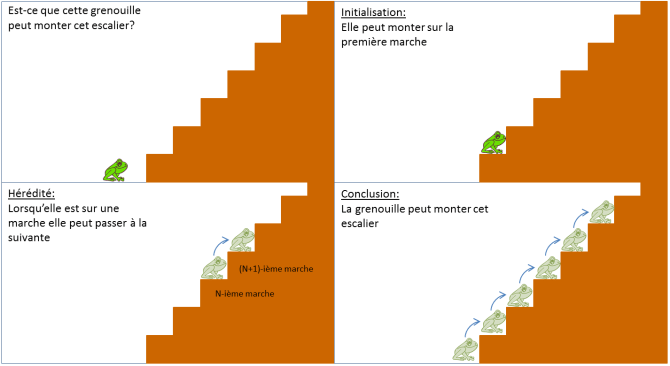
C’est clair? Non? Relire lentement la phrase précédente… Si oui, on passe à la suite.

J’entends déjà des voix s’élever pour me dire « Bon ok mais c’est quoi le rapport entre les escaliers et mon cours de maths?? ». On se calme, ça vient…Dans la phrase écrite en gras j’ai 3 étapes que je vais vous regrouper dans un tableau:

Initialisation	SI il existe un entier n0 tel que P(n0) est vraie	Je peux monter sur la première marche de l’escalier
Hérédité	ET pour tout entier n≥n0, P(n)⇒P(n+1)	Quand je suis sur une marche je peux passer à la suivante
Conclusion	ALORS pour tout n≥n0, P(n) est vraie	Je peux monter l’escalier

Ces trois étapes sont les clés indispensables de tout raisonnement par récurrence digne de ce nom.

A ce stade la seconde colonne est peut être encore un peu floue, alors prenons un exemple:

Soit P(n) la proposition mathématique «1+2+3+…+n=n(n+1)/2 est vraie »

Initialisation :

Si n=1, le terme de gauche vaut 1 et celui de droite aussi, P(1) est donc vérifiée.

Hérédité :

Supposons qu’il existe un entier naturel n pour lequel P(n) est vraie, c’est-à-dire que :

1+2+3+…+n = n(n+1)/2

Démontrons alors que la proposition est vraie au rang n+1, c’est-à-dire que :

1+2+3+…+n+(n+1) = (n+1)(n+2)/2 

Raisonnement : Comme 1+2+3+…+n = n(n+1)/2, alors on peut ajouter  (n+1) de part et d’autre de l’égalité et on obtient :

1+2+3+…+n+(n+1) = n(n+1)/2 +(n+1)

1+2+3+…+n+(n+1) = n(n+1)/2 +2(n+1)/2

1+2+3+…+n+(n+1) = [n(n+1) +2(n+1)]/2

Et en factorisant le terme de droite par (n+1), on obtient:

1+2+3+…+n+(n+1) = (n+1)(n+2)/2

C’est ce que nous souhaitions démontrer. On peut donc en conclure que lorsque la proposition est vraie au rang n elle l’est aussi au rang n+1. C’est-à-dire que P(n)⇒P(n+1).

Conclusion :

P(1) est vraie et pour tout n≥1, P(n)⇒P(n+1) alors P(n) est vraie pour tout n≥1.

Vous avez dû remarquer que l’étape d’hérédité commence par deux choses:

• Une hypothèse, que l’on appelle hypothèse d’hérédité et que l’on trouve après le « supposons que ». C’est notre point de départ pour l’hérédité.
• Ce que l’on veut démontrer, c’est notre point d’arrivé.

Par envie de faire vite ou par flemme d’écrire (ou par soucis écologique, je ne sais pas trop…) vous avez souvent tendance à omettre ces deux points pourtant indispensables. Comment savoir quel chemin prendre pour la démonstration si vous ne savez pas clairement d’où vous partez et où vous allez? C’est impossible en fait… Forcez vous à bien respecter ces étapes et vous aurez déjà fait une bonne partie du boulot.

Voilà, vous savez tout! Vous trouverez ici une fiche imprimable avec l’essentiel sur la récurrence et aussi avec pas mal d’exemples corrigés. Utilisez la pour repérer le raisonnement type! J’y ai surligné en gris les phrases clés qui doivent absolument figurer sur votre copie.